7.4 Winkelsätze und Dreiecke:
Diese rein geometrische Lernumgebung stellt die Sätze zu Winkelsummen im Drei-, Vier- und n-Eck sowie die Winkelbesonderheit im Halbkreis durch den Satz des Thales in den Fokus. Weiter werden die verschiedenen Dreieckformen thematisiert, wobei die Schüler*innen zusätzlich zu den Dreieckeigenschaften bezüglich Seiten und Winkel auch die Konstruktion aller Dreieckformen kennenlernen. Weitere Inhalte dieser Lernumgebung sind Eigenschaften und Konstruktion besonderer Linien und Punkte im Dreieck.
Lernziele und Inhalte: 7.4 Winkelsätze und Dreiecke
Einen größeren Raum nehmen in den Übungen auch problemorientierte Sachaufgaben ein. Mit ihrer Hilfe entsteht für die Schüler*innen ein Bezug zwischen den eingeführten Eigenschaften und ihrem persönlichen Alltag. Dabei ist auch das maßstäbliche Umsetzen von Größen in der Realität auf die Maße im Übungsheft von Bedeutung.
Die vorliegende Übersicht bietet Hinweise zum Aufbau und Einsatz der Unterrichtsreihe und der verschiedenen Inhalte. Ebenso finden sich hier die kompetenzorientierten Lernziele, welche mit den einzelnen Inhalten dieser Lernumgebung aufgebaut, gefördert und/oder vertieft werden können.
Umfang/Länge: 1 Seite
Aus: Lernumgebung Mathematik 7
Fächer: Mathematik
Stufen: 7. Stufe
Kompetenzorientierte Lernziele
- Ich kann die Winkelsumme eines beliebigen Vielecks angeben bzw. durch Rechnung bestimmen.
- Ich kann in Drei-, Vier- und n-Ecken fehlende Winkel über die Winkelsummensätze berechnen.
- Ich kann in komplexen geradlinig begrenzten Figuren fehlende Winkel über die Winkelsätze berechnen.
- Ich kann den Satz des Thales bei Winkelberechnungen und Konstruktionen anwenden.
- Ich kann die verschiedenen Dreieckformen bezüglich ihrer Eigenschaften benennen und unterscheiden.
- Ich kann den Winkelsummensatz auch in den Sonderformen des Dreiecks anwenden.
- Ich kann allgemeine Dreiecke mithilfe von gegebenen Seiten und Winkeln konstruieren.
- Ich kann Dreiecksonderformen mithilfe von gegebenen Seiten und Winkeln konstruieren.
- Ich kann die besonderen Eigenschaften des Umkreis- und Inkreismittelpunkts verstehen und erläutern.
- Ich kann den Umkreis- und Inkreismittelpunkt sowie den Höhenschnittpunkt von Dreiecken konstruieren.
- Ich kann Dreiecke auch mithilfe von Umkreisradius, einer Winkelhalbierenden oder Höhe konstruieren.
- Ich kann Dreieckskonstruktionen in alltagsbezogenen Anwendungen maßstäblich durchführen.
Einschätzungsbogen für Lehrpersonen und Schüler*innen, der formativ während dem Lernprozess oder am Schluss als Teil der summativen Kompetenzbeurteilung eingesetzt werden kann. Erstellt mit dem IQES-Lernkompass.
Umfang/Länge: 1 Seite
Aus: Lernumgebung Mathematik 7
Fächer: Mathematik
Stufen: 7. Stufe
Einschätzungsbogen für Schüler*innen. Erstellt mit dem IQES-Lernkompass.
Umfang/Länge: 1 Seite
Aus: Lernumgebung Mathematik 7
Fächer: Mathematik
Stufen: 7. Stufe
UA
Übungsaufgaben, Regeleinträge und Videos: Übungsaufgaben auf drei Schwierigkeitsgraden ermöglichen differenzierte Lernangebote. Regeleinträge und Videos bieten in kompakter Form das notwendige Basiswissen.
7.4.1 Winkelansätze und Winkelsummen – Regeleintrag
Inhaltliches Basiswissen für Lernende (Eintrag ins Lerntagebuch, Wissenskartei, Spickkarten, …). Die Regeleinträge können als wichtige Begleiter beim Lösen der verschiedenen Aufgaben genutzt werden.
Autor/Autorin: Gernot Braun

Gernot Braun war von 1977 bis 2016 als Realschullehrer mit den Fächern Mathematik und Sport an der Realschule Wolfach (Ortenaukreis) tätig und ab 2005 auch als Konrektor an der gleichen Schule. Seit seinem Ruhestand erstellte er alle Materialien in Mathematik für die Realschule Wolfach und sekundär für Klasse 10 auch für die Realschule Triberg.
Umfang/Länge: 3 Seiten
Aus: Lernumgebung Mathematik 7
Fächer: Mathematik
Stufen: 7. Stufe
7.4.1 Winkelansätze und Winkelsummen – Übungsaufgaben
Nach drei Schwierigkeitsstufen differenzierte Lernaufgaben. Lehrpersonen und Schüler*innen können aus der Aufgabensammlung leichte, mittlere oder schwierige Aufgaben auswählen und Wege für individuelles Lernen und Üben eröffnen.
Autor/Autorin: Gernot Braun

Gernot Braun war von 1977 bis 2016 als Realschullehrer mit den Fächern Mathematik und Sport an der Realschule Wolfach (Ortenaukreis) tätig und ab 2005 auch als Konrektor an der gleichen Schule. Seit seinem Ruhestand erstellte er alle Materialien in Mathematik für die Realschule Wolfach und sekundär für Klasse 10 auch für die Realschule Triberg.
Umfang/Länge: 6 Seiten
Aus: Lernumgebung Mathematik 7
Fächer: Mathematik
Stufen: 7. Stufe
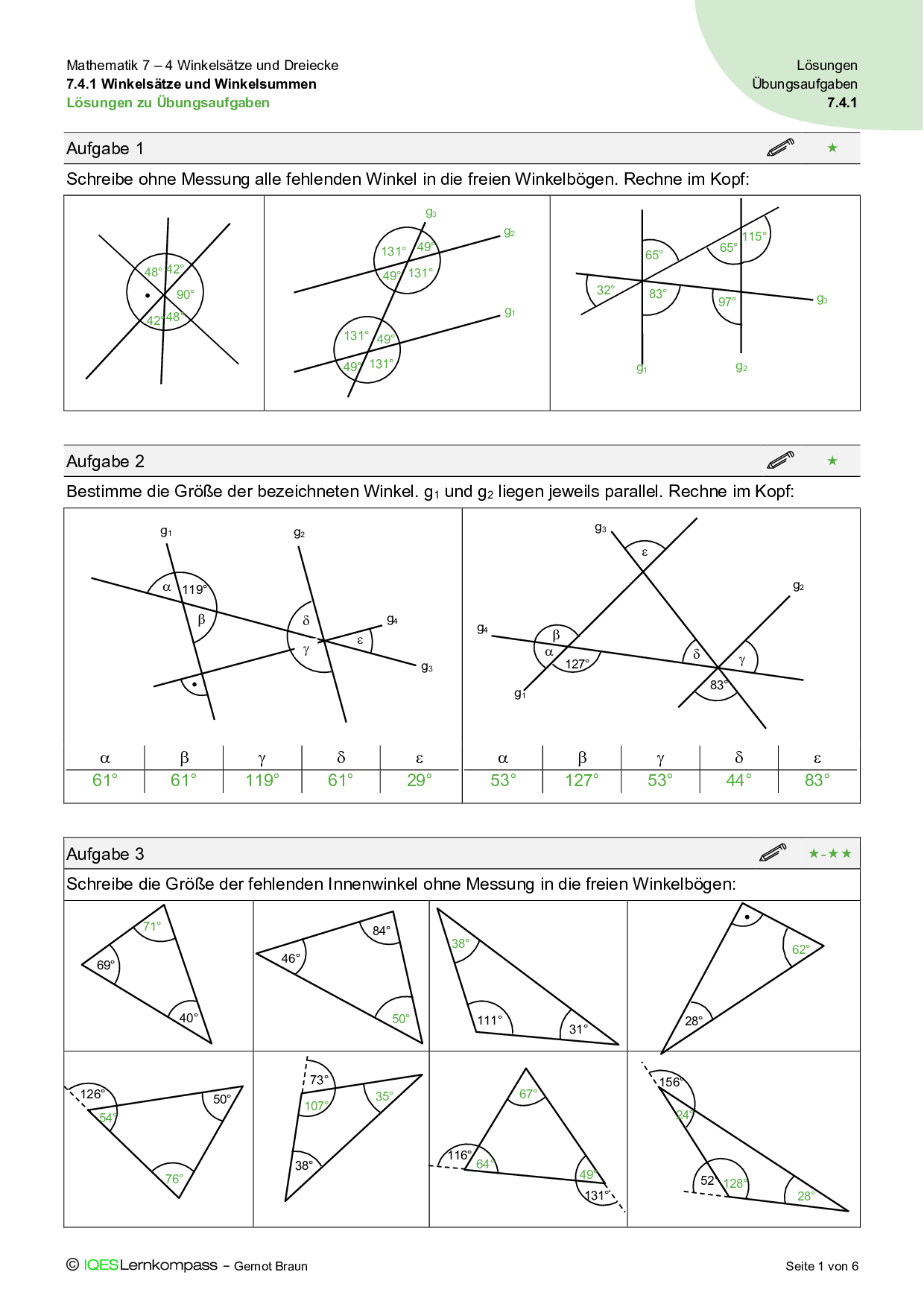
7.4.1 Winkelansätze und Winkelsummen – Übungsaufgaben mit Lösungen
Lösungsblätter zu allen Übungsaufgaben ermöglichen sowohl Selbst- wie auch Fremdkontrolle als methodische Möglichkeiten zur Überprüfung.
Autor/Autorin: Gernot Braun

Gernot Braun war von 1977 bis 2016 als Realschullehrer mit den Fächern Mathematik und Sport an der Realschule Wolfach (Ortenaukreis) tätig und ab 2005 auch als Konrektor an der gleichen Schule. Seit seinem Ruhestand erstellte er alle Materialien in Mathematik für die Realschule Wolfach und sekundär für Klasse 10 auch für die Realschule Triberg.
Umfang/Länge: 6 Seiten
Aus: Lernumgebung Mathematik 7
Fächer: Mathematik
Stufen: 7. Stufe
Erklärvideos

Realschule Europakanal: Tutorial: Arten von Dreiecken und Innenwinkelsumme
7.4.2 Dreieckformen – Regeleintrag
Inhaltliches Basiswissen für Lernende (Eintrag ins Lerntagebuch, Wissenskartei, Spickkarten, …). Die Regeleinträge können als wichtige Begleiter beim Lösen der verschiedenen Aufgaben genutzt werden.
Umfang/Länge: 2 Seiten
Aus: Lernumgebung Mathematik 7
Fächer: Mathematik
Stufen: 7. Stufe
7.4.2 Dreieckformen – Übungsaufgaben
Nach drei Schwierigkeitsstufen differenzierte Lernaufgaben. Lehrpersonen und Schüler*innen können aus der Aufgabensammlung leichte, mittlere oder schwierige Aufgaben auswählen und Wege für individuelles Lernen und Üben eröffnen.
Umfang/Länge: 4 Seiten
Aus: Lernumgebung Mathematik 7
Fächer: Mathematik
Stufen: 7. Stufe
7.4.2 Dreieckformen – Übungsaufgaben mit Lösungen
Lösungsblätter zu allen Übungsaufgaben ermöglichen sowohl Selbst- wie auch Fremdkontrolle als methodische Möglichkeiten zur Überprüfung.
Autor/Autorin: Gernot Braun

Gernot Braun war von 1977 bis 2016 als Realschullehrer mit den Fächern Mathematik und Sport an der Realschule Wolfach (Ortenaukreis) tätig und ab 2005 auch als Konrektor an der gleichen Schule. Seit seinem Ruhestand erstellte er alle Materialien in Mathematik für die Realschule Wolfach und sekundär für Klasse 10 auch für die Realschule Triberg.
Umfang/Länge: 3 Seiten
Aus: Lernumgebung Mathematik 7
Fächer: Mathematik
Stufen: 7. Stufe
Erklärvideos

Lehrerschmidt: Dreieck rechtwinklig – gleichseitig – gleichschenklig
7.4.3 Dreieckkonstruktionen – Regeleintrag
Inhaltliches Basiswissen für Lernende (Eintrag ins Lerntagebuch, Wissenskartei, Spickkarten, …). Die Regeleinträge können als wichtige Begleiter beim Lösen der verschiedenen Aufgaben genutzt werden.
Autor/Autorin: Gernot Braun

Gernot Braun war von 1977 bis 2016 als Realschullehrer mit den Fächern Mathematik und Sport an der Realschule Wolfach (Ortenaukreis) tätig und ab 2005 auch als Konrektor an der gleichen Schule. Seit seinem Ruhestand erstellte er alle Materialien in Mathematik für die Realschule Wolfach und sekundär für Klasse 10 auch für die Realschule Triberg.
Umfang/Länge: 4 Seiten
Aus: Lernumgebung Mathematik 7
Fächer: Mathematik
Stufen: 7. Stufe
7.4.3 Dreieckkonstruktionen – Übungsaufgaben
Nach drei Schwierigkeitsstufen differenzierte Lernaufgaben. Lehrpersonen und Schüler*innen können aus der Aufgabensammlung leichte, mittlere oder schwierige Aufgaben auswählen und Wege für individuelles Lernen und Üben eröffnen.
Autor/Autorin: Gernot Braun

Gernot Braun war von 1977 bis 2016 als Realschullehrer mit den Fächern Mathematik und Sport an der Realschule Wolfach (Ortenaukreis) tätig und ab 2005 auch als Konrektor an der gleichen Schule. Seit seinem Ruhestand erstellte er alle Materialien in Mathematik für die Realschule Wolfach und sekundär für Klasse 10 auch für die Realschule Triberg.
Umfang/Länge: 5 Seiten
Aus: Lernumgebung Mathematik 7
Fächer: Mathematik
Stufen: 7. Stufe
7.4.3 Dreieckkonstruktionen – Übungsaufgaben mit Lösungen
Lösungsblätter zu allen Übungsaufgaben ermöglichen sowohl Selbst- wie auch Fremdkontrolle als methodische Möglichkeiten zur Überprüfung.
Autor/Autorin: Gernot Braun

Gernot Braun war von 1977 bis 2016 als Realschullehrer mit den Fächern Mathematik und Sport an der Realschule Wolfach (Ortenaukreis) tätig und ab 2005 auch als Konrektor an der gleichen Schule. Seit seinem Ruhestand erstellte er alle Materialien in Mathematik für die Realschule Wolfach und sekundär für Klasse 10 auch für die Realschule Triberg.
Umfang/Länge: 12 Seiten
Aus: Lernumgebung Mathematik 7
Fächer: Mathematik
Stufen: 7. Stufe
Erklärvideos

Mathe by Daniel Jung: Konstruktion Dreieck, Ablauf, SSS, SWS, SSW, WSW, Geometrie
7.4.4 Besondere Linien und Punkte im Dreieck – Regeleintrag
Inhaltliches Basiswissen für Lernende (Eintrag ins Lerntagebuch, Wissenskartei, Spickkarten, …). Die Regeleinträge können als wichtige Begleiter beim Lösen der verschiedenen Aufgaben genutzt werden.
Autor/Autorin: Gernot Braun

Gernot Braun war von 1977 bis 2016 als Realschullehrer mit den Fächern Mathematik und Sport an der Realschule Wolfach (Ortenaukreis) tätig und ab 2005 auch als Konrektor an der gleichen Schule. Seit seinem Ruhestand erstellte er alle Materialien in Mathematik für die Realschule Wolfach und sekundär für Klasse 10 auch für die Realschule Triberg.
Umfang/Länge: 4 Seiten
Aus: Lernumgebung Mathematik 7
Fächer: Mathematik
Stufen: 7. Stufe
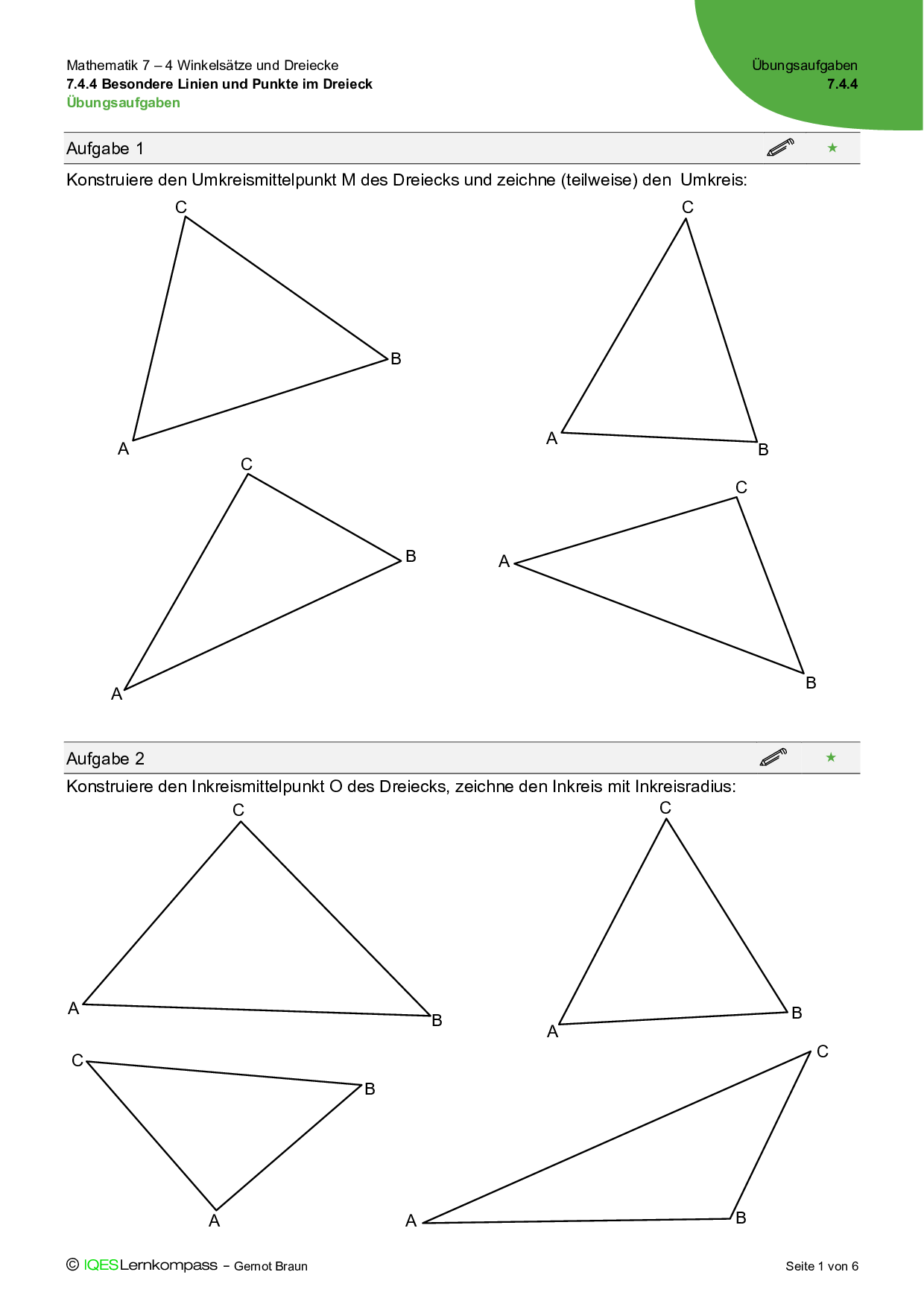
7.4.4 Besondere Linien und Punkte im Dreieck – Übungsaufgaben
Nach drei Schwierigkeitsstufen differenzierte Lernaufgaben. Lehrpersonen und Schüler*innen können aus der Aufgabensammlung leichte, mittlere oder schwierige Aufgaben auswählen und Wege für individuelles Lernen und Üben eröffnen.
Autor/Autorin: Gernot Braun

Gernot Braun war von 1977 bis 2016 als Realschullehrer mit den Fächern Mathematik und Sport an der Realschule Wolfach (Ortenaukreis) tätig und ab 2005 auch als Konrektor an der gleichen Schule. Seit seinem Ruhestand erstellte er alle Materialien in Mathematik für die Realschule Wolfach und sekundär für Klasse 10 auch für die Realschule Triberg.
Umfang/Länge: 6 Seiten
Aus: Lernumgebung Mathematik 7
Fächer: Mathematik
Stufen: 7. Stufe
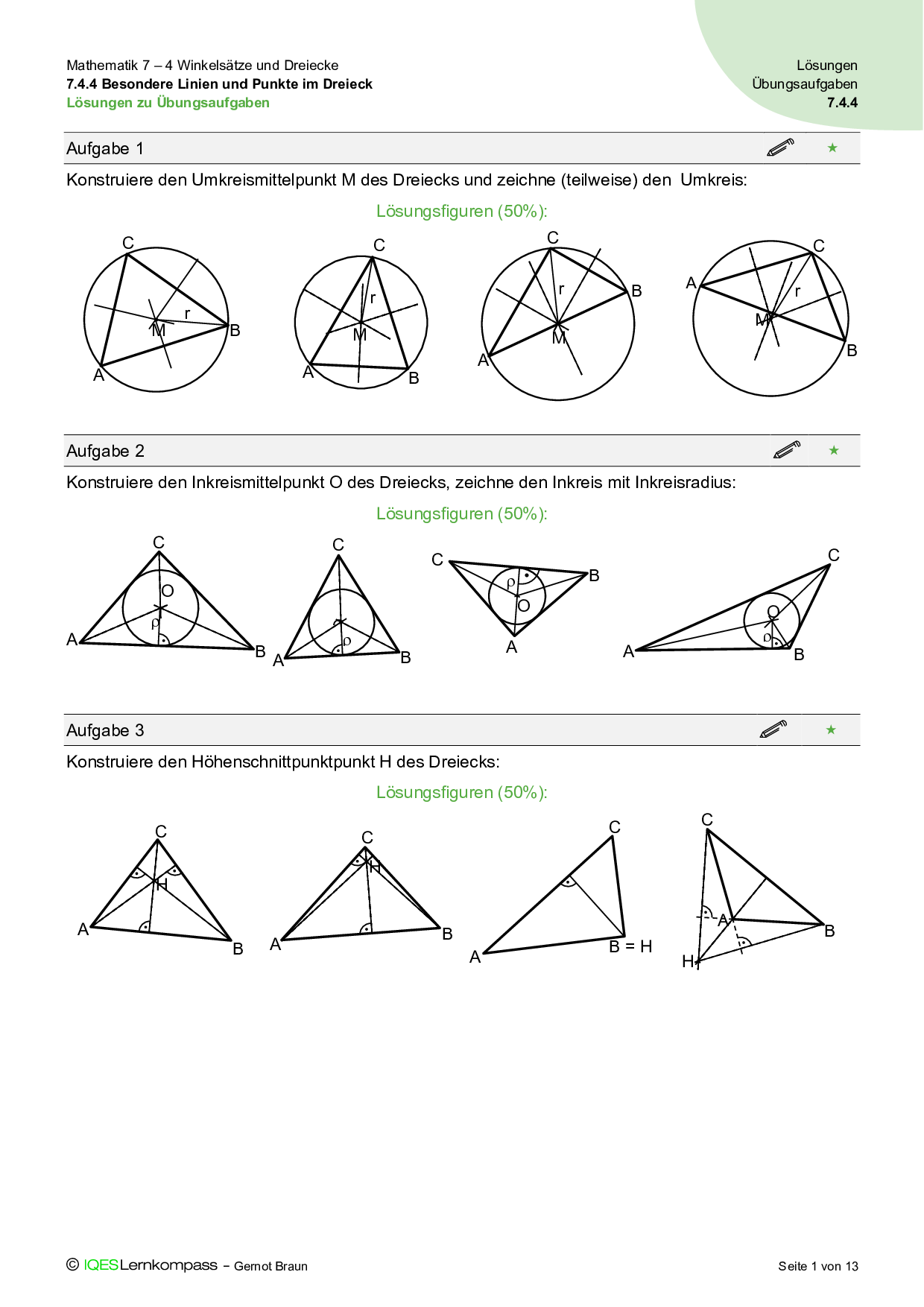
7.4.4 Besondere Linien und Punkte im Dreieck – Übungsaufgaben mit Lösungen
Lösungsblätter zu allen Übungsaufgaben ermöglichen sowohl Selbst- wie auch Fremdkontrolle als methodische Möglichkeiten zur Überprüfung.
Autor/Autorin: Gernot Braun

Gernot Braun war von 1977 bis 2016 als Realschullehrer mit den Fächern Mathematik und Sport an der Realschule Wolfach (Ortenaukreis) tätig und ab 2005 auch als Konrektor an der gleichen Schule. Seit seinem Ruhestand erstellte er alle Materialien in Mathematik für die Realschule Wolfach und sekundär für Klasse 10 auch für die Realschule Triberg.
Umfang/Länge: 13 Seiten
Aus: Lernumgebung Mathematik 7
Fächer: Mathematik
Stufen: 7. Stufe
Erklärvideos

Schoolseasy: Besondere Linien im Dreieck
LT
Lerntests: Die Lerntests sind als zwischenzeitliche formative Lernkontrolle des gesamten Kapitels gedacht. Sie sind in drei Schwierigkeitsstufen aufgeteilt, wobei Lerntest C die anspruchsvollste Variante ist. Die Lerntests stehen jeweils in 2 Varianten (mit oder ohne Lösungen) zur Verfügung.
7.4 Winkelsätze und Dreiecke – Lerntest A
Formative Lernkontrolle: einfache Variante
Autor/Autorin: Gernot Braun

Gernot Braun war von 1977 bis 2016 als Realschullehrer mit den Fächern Mathematik und Sport an der Realschule Wolfach (Ortenaukreis) tätig und ab 2005 auch als Konrektor an der gleichen Schule. Seit seinem Ruhestand erstellte er alle Materialien in Mathematik für die Realschule Wolfach und sekundär für Klasse 10 auch für die Realschule Triberg.
Umfang/Länge: 3 Seiten
Aus: Lernumgebung Mathematik 7
Fächer: Mathematik
Stufen: 7. Stufe
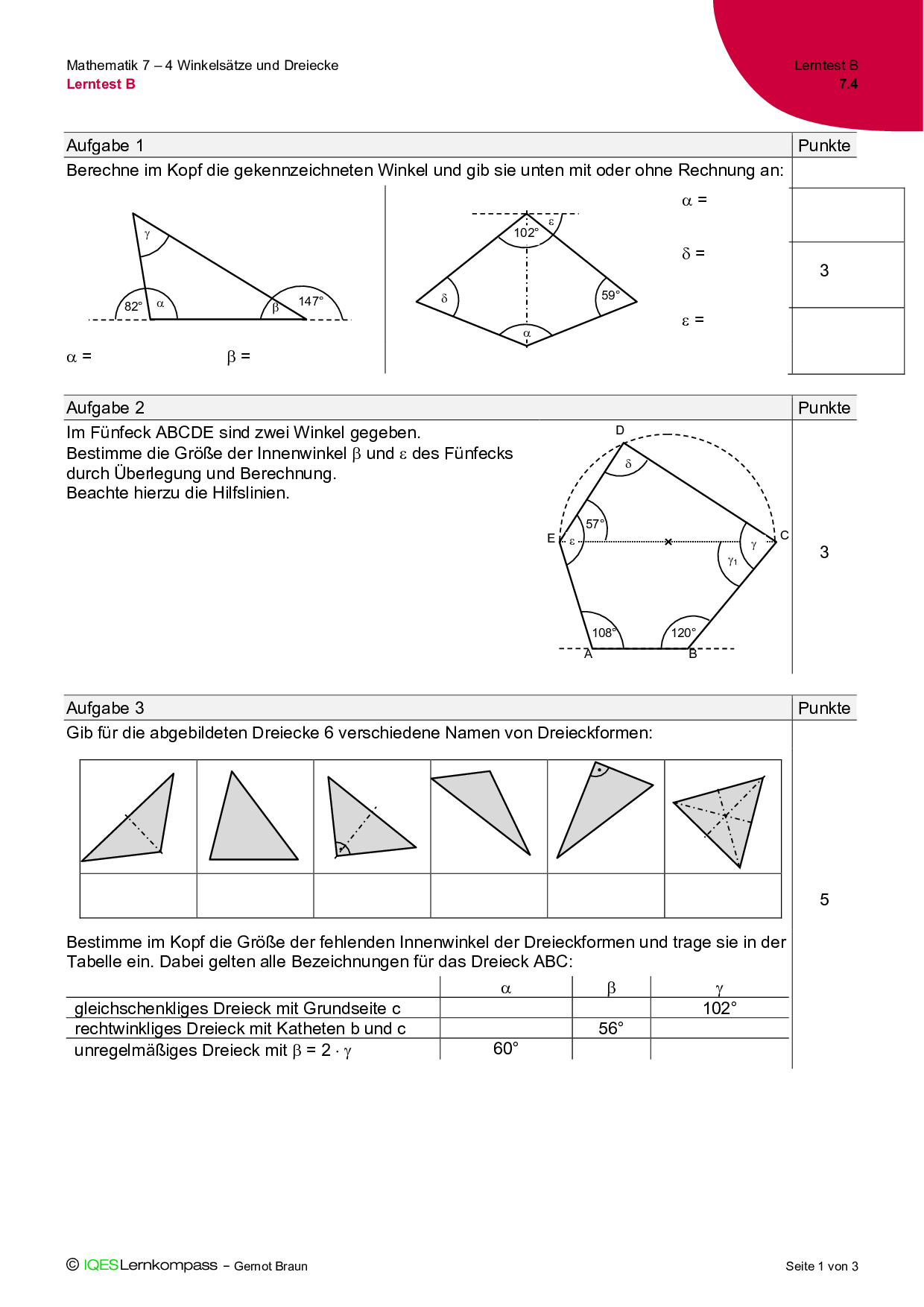
7.4 Winkelsätze und Dreiecke – Lerntest B
Formative Lernkontrolle: mittlere Variante
Autor/Autorin: Gernot Braun

Gernot Braun war von 1977 bis 2016 als Realschullehrer mit den Fächern Mathematik und Sport an der Realschule Wolfach (Ortenaukreis) tätig und ab 2005 auch als Konrektor an der gleichen Schule. Seit seinem Ruhestand erstellte er alle Materialien in Mathematik für die Realschule Wolfach und sekundär für Klasse 10 auch für die Realschule Triberg.
Umfang/Länge: 3 Seiten
Aus: Lernumgebung Mathematik 7
Fächer: Mathematik
Stufen: 7. Stufe
7.4 Winkelsätze und Dreiecke – Lerntest C
Formative Lernkontrolle: schwierige Variante
Autor/Autorin: Gernot Braun

Gernot Braun war von 1977 bis 2016 als Realschullehrer mit den Fächern Mathematik und Sport an der Realschule Wolfach (Ortenaukreis) tätig und ab 2005 auch als Konrektor an der gleichen Schule. Seit seinem Ruhestand erstellte er alle Materialien in Mathematik für die Realschule Wolfach und sekundär für Klasse 10 auch für die Realschule Triberg.
Umfang/Länge: 4 Seiten
Aus: Lernumgebung Mathematik 7
Fächer: Mathematik
Stufen: 7. Stufe
7.4 Winkelsätze und Dreiecke – Lösungen zum Lerntest A
Lösungen zu den Aufgaben des Lerntests A (einfache Variante) für die Selbst- und Fremdkontrolle
Autor/Autorin: Gernot Braun

Gernot Braun war von 1977 bis 2016 als Realschullehrer mit den Fächern Mathematik und Sport an der Realschule Wolfach (Ortenaukreis) tätig und ab 2005 auch als Konrektor an der gleichen Schule. Seit seinem Ruhestand erstellte er alle Materialien in Mathematik für die Realschule Wolfach und sekundär für Klasse 10 auch für die Realschule Triberg.
Umfang/Länge: 3 Seiten
Aus: Lernumgebung Mathematik 7
Fächer: Mathematik
Stufen: 7. Stufe
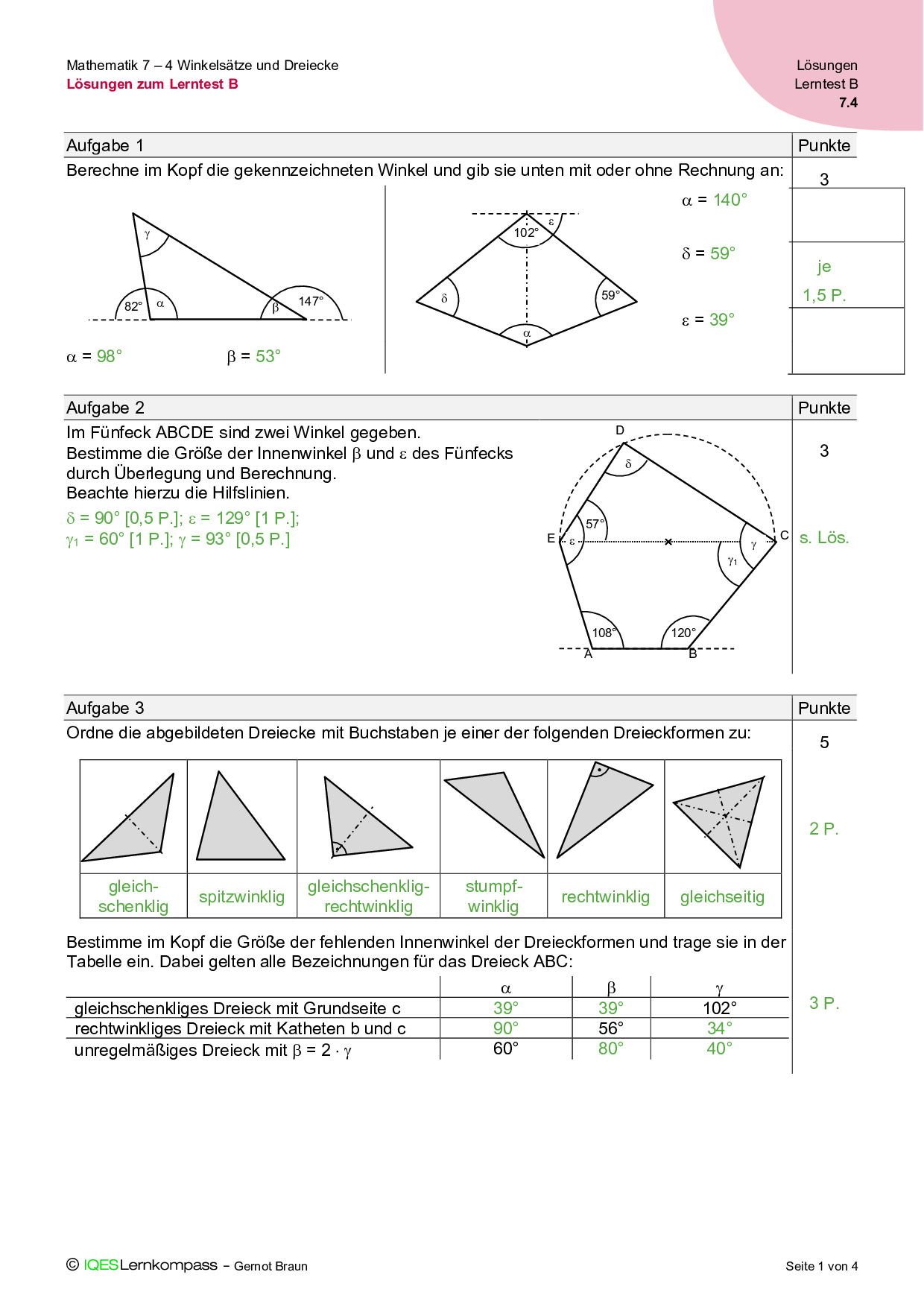
7.4 Winkelsätze und Dreiecke – Lösungen zum Lerntest B
Lösungen zu den Aufgaben des Lerntests B (mittlere Variante) für die Selbst- und Fremdkontrolle
Autor/Autorin: Gernot Braun

Gernot Braun war von 1977 bis 2016 als Realschullehrer mit den Fächern Mathematik und Sport an der Realschule Wolfach (Ortenaukreis) tätig und ab 2005 auch als Konrektor an der gleichen Schule. Seit seinem Ruhestand erstellte er alle Materialien in Mathematik für die Realschule Wolfach und sekundär für Klasse 10 auch für die Realschule Triberg.
Umfang/Länge: 4 Seiten
Aus: Lernumgebung Mathematik 7
Fächer: Mathematik
Stufen: 7. Stufe
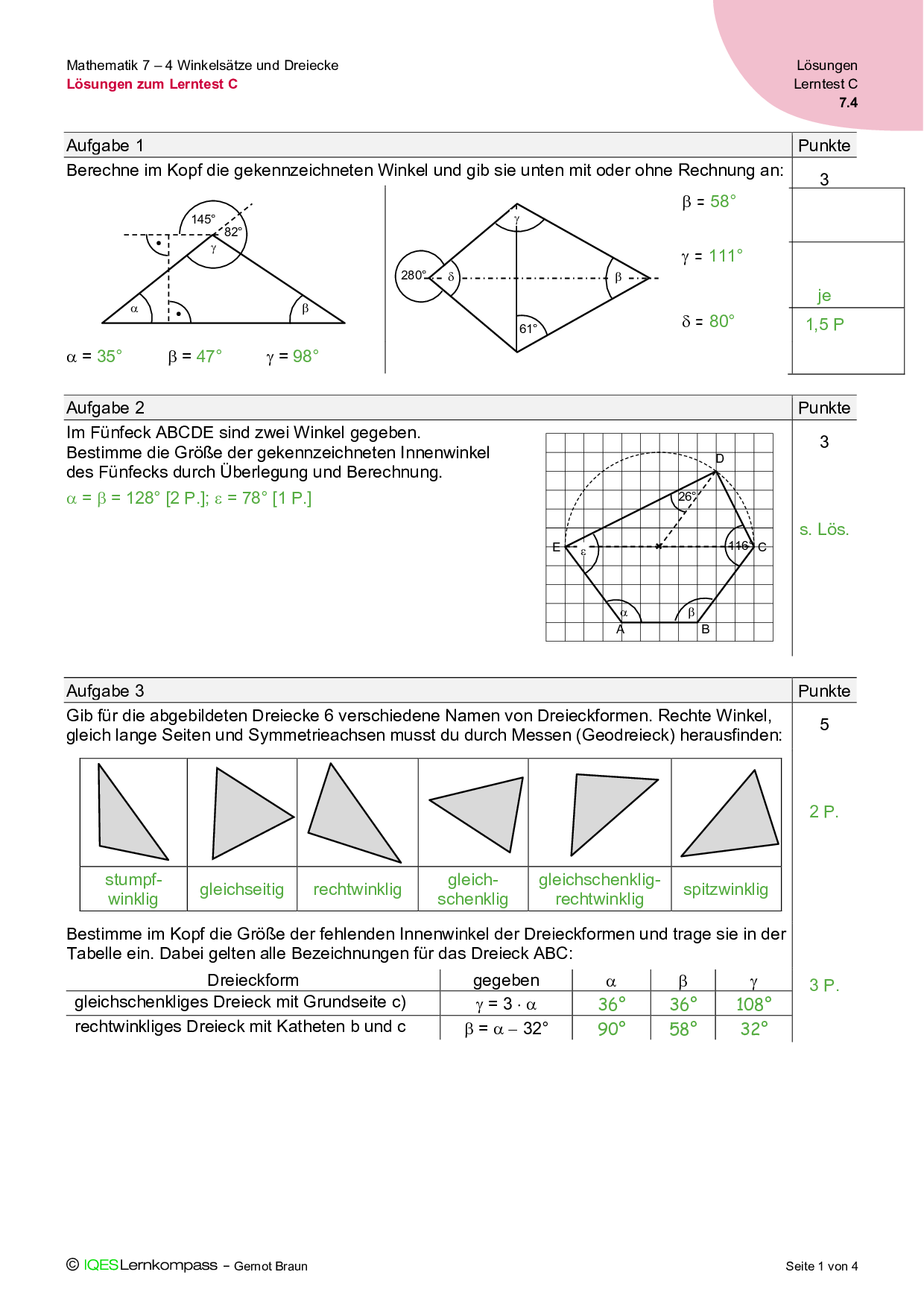
7.4 Winkelsätze und Dreiecke – Lösungen zum Lerntest C
Lösungen zu den Aufgaben des Lerntests C (schwierige Variante) für die Selbst- und Fremdkontrolle
Autor/Autorin: Gernot Braun

Gernot Braun war von 1977 bis 2016 als Realschullehrer mit den Fächern Mathematik und Sport an der Realschule Wolfach (Ortenaukreis) tätig und ab 2005 auch als Konrektor an der gleichen Schule. Seit seinem Ruhestand erstellte er alle Materialien in Mathematik für die Realschule Wolfach und sekundär für Klasse 10 auch für die Realschule Triberg.
Umfang/Länge: 4 Seiten
Aus: Lernumgebung Mathematik 7
Fächer: Mathematik
Stufen: 7. Stufe
RS
Rückspiegel: Der Rückspiegel eröffnet (nach den Erkenntnissen aus dem Lerntest) die nächsten Lernschritte. Je nach Lernstand können bestimmte mathematische Muster und Konzepte nochmals erkundet, systematisiert und gesichert werden. Der Rückspiegel bietet Aufgaben zum Üben, Vertiefen und Wiederholen an und macht damit eine individualisierte Vorbereitung und Lernbegleitung auf den Abschlusstest möglich.
7.4 Winkelsätze und Dreiecke – Rückspiegel
Aufgaben zur individuellen Vorbereitung auf den Abschlusstest
Umfang/Länge: 6 Seiten
Aus: Lernumgebung Mathematik 7
Fächer: Mathematik
Stufen: 7. Stufe
7.4 Winkelsätze und Dreiecke – Lösungen zum Rückspiegel
Aufgaben mit Lösungen zur individuellen Vorbereitung auf den Abschlusstest
Autor/Autorin: Gernot Braun

Gernot Braun war von 1977 bis 2016 als Realschullehrer mit den Fächern Mathematik und Sport an der Realschule Wolfach (Ortenaukreis) tätig und ab 2005 auch als Konrektor an der gleichen Schule. Seit seinem Ruhestand erstellte er alle Materialien in Mathematik für die Realschule Wolfach und sekundär für Klasse 10 auch für die Realschule Triberg.
Umfang/Länge: 16 Seiten
Aus: Lernumgebung Mathematik 7
Fächer: Mathematik
Stufen: 7. Stufe
AT
Abschlusstest: Lehrpersonen finden hier eine Aufgabensammlung, aus der sie einen auf den Lernstand der Klasse zugeschnittenen Abschlusstest zusammenstellen und auf diese Weise den Leistungsstand der einzelnen Schüler*innen und der ganzen Klasse summativ beurteilen können.
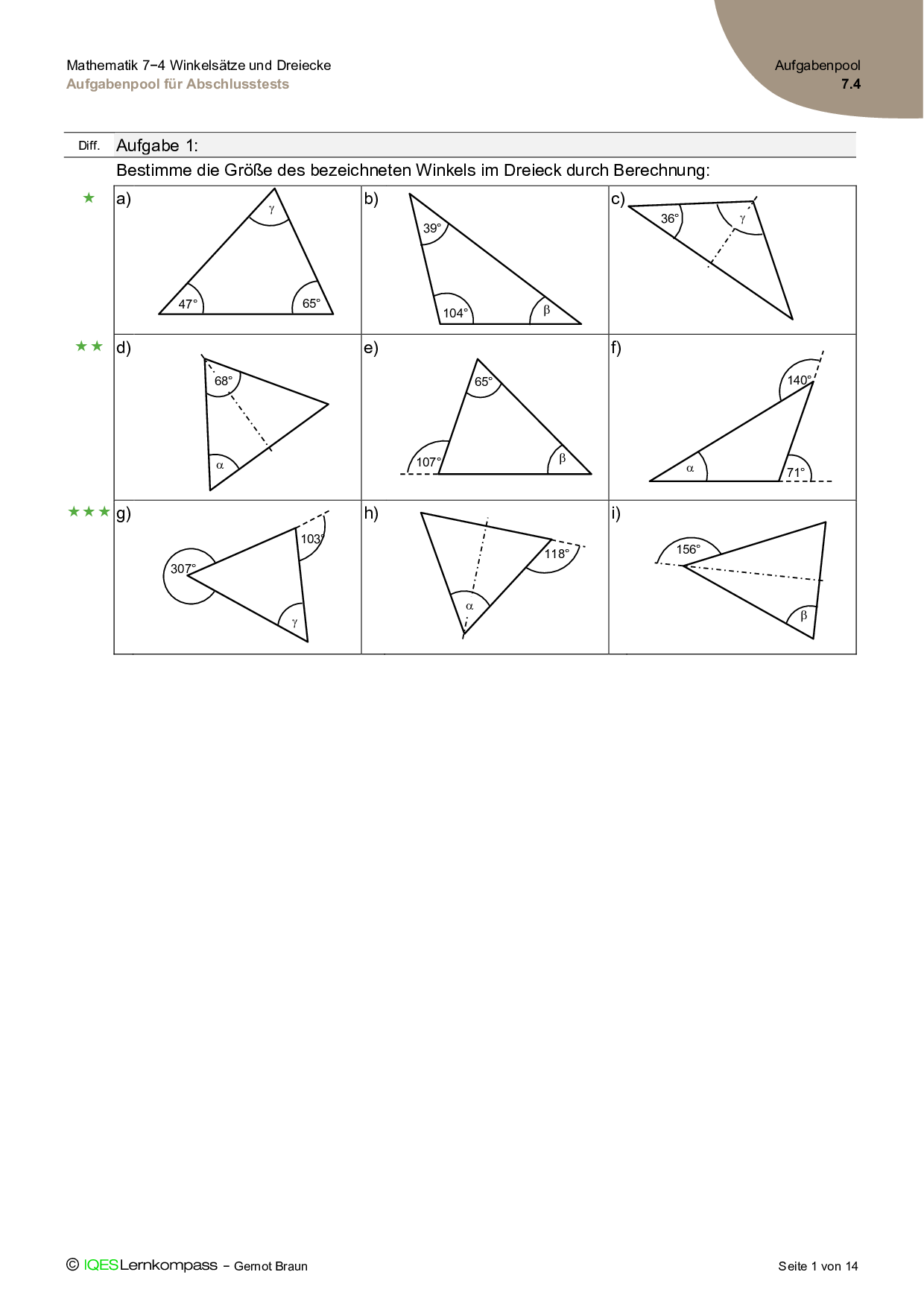
7.4 Winkelsätze und Dreiecke – Aufgabenpool für Abschlusstests
Nach drei Schwierigkeitsstufen differenzierte Aufgabensammlung für die Zusammenstellung von Abschlusstests durch die Lehrperson.
Autor/Autorin: Gernot Braun

Gernot Braun war von 1977 bis 2016 als Realschullehrer mit den Fächern Mathematik und Sport an der Realschule Wolfach (Ortenaukreis) tätig und ab 2005 auch als Konrektor an der gleichen Schule. Seit seinem Ruhestand erstellte er alle Materialien in Mathematik für die Realschule Wolfach und sekundär für Klasse 10 auch für die Realschule Triberg.
Umfang/Länge: 14 Seiten
Aus: Lernumgebung Mathematik 7
Fächer: Mathematik
Stufen: 7. Stufe
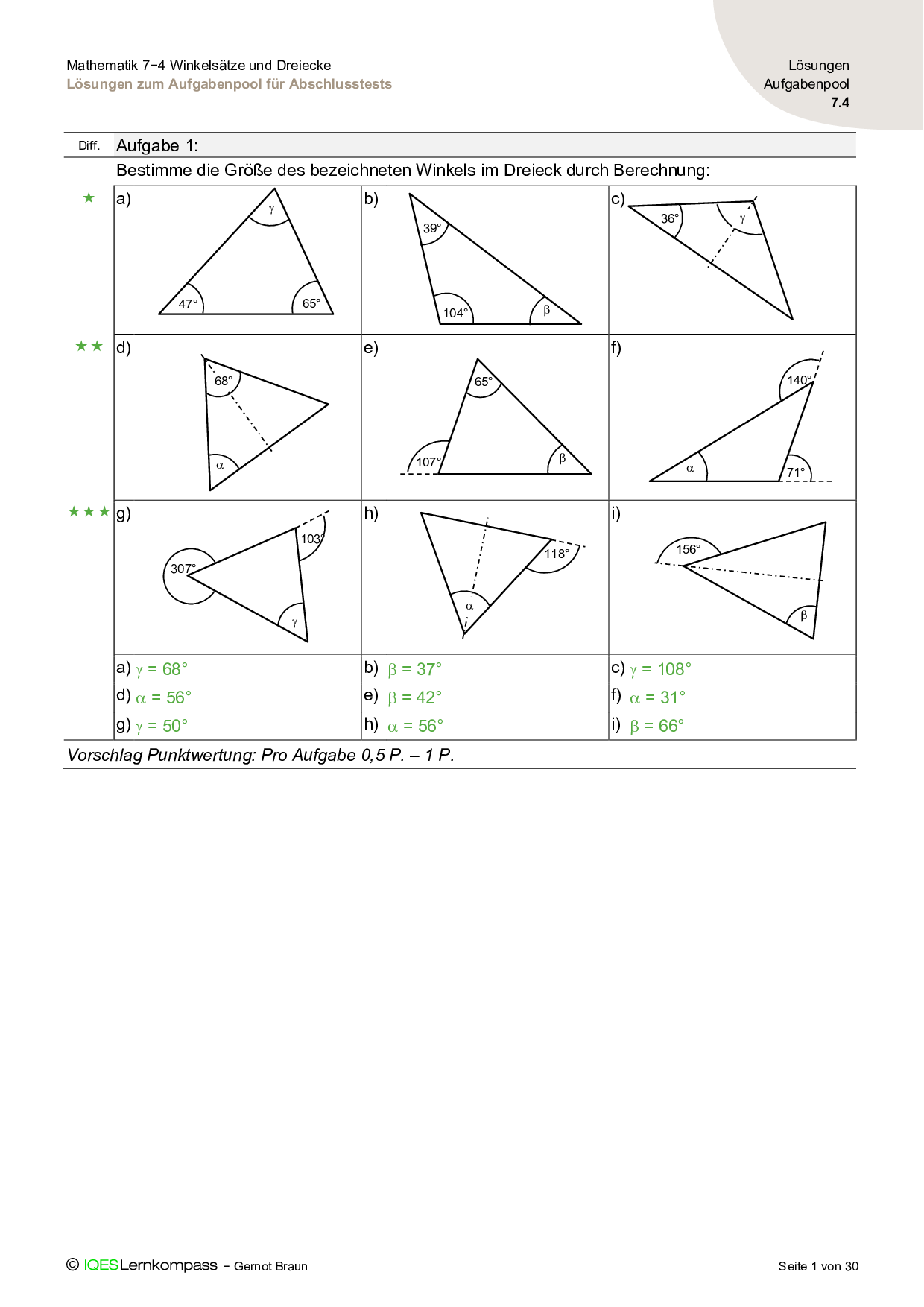
7.4 Winkelsätze und Dreiecke – Lösungen zum Aufgabenpool für Abschlusstests
Lösungen zur Aufgabensammlung für Abschlusstests.
Autor/Autorin: Gernot Braun

Gernot Braun war von 1977 bis 2016 als Realschullehrer mit den Fächern Mathematik und Sport an der Realschule Wolfach (Ortenaukreis) tätig und ab 2005 auch als Konrektor an der gleichen Schule. Seit seinem Ruhestand erstellte er alle Materialien in Mathematik für die Realschule Wolfach und sekundär für Klasse 10 auch für die Realschule Triberg.
Umfang/Länge: 30 Seiten
Aus: Lernumgebung Mathematik 7
Fächer: Mathematik
Stufen: 7. Stufe